Webプログラミング学習

只今、webプログラミングの勉強中！
基礎科学をテーマにしてwebプログラミングを学ぼう！

　20年前に当館のホームページを開設して以来ずっと更新を続けてきましたが、HTMLのコーディングばかりでHP作成技術にさっぱり進歩がないので、HTML以外のWebプログラミングも勉強しながらコツコツと当館のHPを進歩発展させていこうと思います。
　「JavaScript」などのWebプログラミング用の言語はブラウザで翻訳してブラウザ上で実行できるもので、めんどうな準備もなく誰でもプログラミング学習を始めることのできる入門的な言語だと思います。

注意：
　下記の記事(リンク先の記事も)は、InternetExprolerの8以前のバージョンでは正しく表示できません。　また、スマホなどのモバイル機器で閲覧するとブラウザがフリーズ(凍結)してしまう恐れがあります。　なるべくパソコンをご使用ください。

　Windowsを使っている方には、Windows版のFirefoxやGoogleChromeなどのブラウザをお勧めします。
　下記の記事(リンク先の記事も)は、Linux上でFirefoxを使って確認していますが、他のブラウザでは若干ないしは大変表示が異なっているかもしれません。

　　　　過去に掲載の関連記事
★令和1年6月1日更新の表紙ページへリンク
★令和1年6月5日更新の表紙ページへリンク
★令和1年6月24日更新の表紙ページへリンク
★令和1年7月23日更新の表紙ページへリンク
★令和1年9月29日更新の表紙ページへリンク
★令和2年8月19日更新の表紙ページへリンク

只今、webプログラミングの勉強中！
ケプラーの法則で学ぶwebプログラミング

　数学や物理、化学は自然科学のどの分野にも必要な基礎科学で、基礎科学が必要ないような自然科学などはないはずなので、当館も基礎科学を大事にしたいと思います。　これからも基礎科学的なテーマでプログラムの勉強をしてみたいと思います。

黄道にほぼ沿って並ぶ「木星」「土星」「火星」「天王星」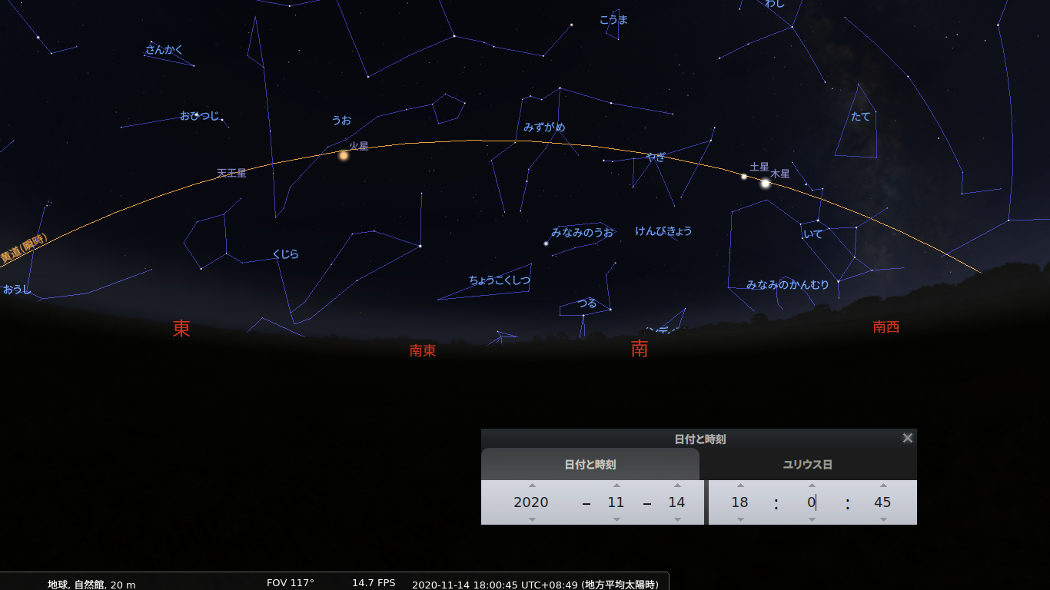

　上の画像は、天文シミュレーションソフト「ステラリウム」からスクリーンショットしたものです。　黄色の線で表示されているのが「黄道」で、時々刻々日ごとに黄道上を太陽の位置が東へ移動していき、一年後には一周してもとの位置に戻ってきます。　つまり、黄道は太陽が一年かかって天球上を一周する道筋で、地球の公転軌道面を天球へ投影したものに相当します。　そして、地球以外の火星、木星、土星などの惑星も黄道にほぼ沿って移動することから、これらの惑星の公転軌道面も地球の公転軌道面とほぼ重なった位置関係にあることがわかります。

楕円を考えよう！・・・楕円の方程式の導出

クリック！

楕円内部の二つの赤い点は楕円の焦点です。

長半径と短半径をいろいろ変えて楕円を表示してみてください！
x方向の半径：0250 y方向の半径：0250	長半径200 短半径150

楕円とは・・・楕円の定義

「平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線を楕円という。　この2定点を焦点という。」

　　

　楕円の説明図1では、長半径200、短半径150の楕円を表示しています。　図中の2点F1、F2は楕円の焦点で、点Pは楕円上の任意の点です。

　点P、F1間の長さPF1、点P、F2間の長さPF2より、楕円は　PF1+PF2=(一定)　という関係を成り立たせる点Pの集合でできている曲線といえます。

　　　　　　

　説明図2において、
線分ACは2つの焦点F1、F2を通り楕円と交わる点を端点とする線分、つまり楕円の長径で、線分BDは線分ACを垂直二等分し楕円と交わる点を端点とする線分、つまり楕円の短径です。

点pがちょうど点Aの位置にあるときを考えてみると、PF1+PF2=PF1+PF1+F1F2=2(PF1)+F1F2=2(AF1)+F1F2
点pがちょうど点Cの位置にあるときを考えてみると、PF1+PF2=PF2+F1F2+PF2=2(PF2)+F1F2=2(CF2)+F1F2
したがって、2(AF1)+F1F2=2(CF2)+F1F2 → AF1=CF2 であることが証明でき、PF1+PF2=AF1+CF2+F1F2=AC となります。
つまり、楕円の定義の PF1+PF2=(一定) の式にある(一定)は線分AC(長径)の長さのことで、PF1+PF2=(長径) であることがわかります。

　点pがちょうど点Bの位置にあるときを考えてみると、線分BDは線分ACを垂直二等分するものなので OF1=OF2、
したがって、三角形POF1と三角形POF2とは合同関係で PF1=PF2 なので、PF1+PF2=2(PF1)=2(PF2)=(長径) → PF1=PF2=

\frac{1}{2}

(長径)=(長半径)
つまり、点Pが点Bの位置にあるときには PF1=PF2=(長半径) となり、PF1=BF1、PF2=BF2 なので BF1=BF2=(長半径) であることがわかります。
　また、点Pが点Dの位置にあるときも考えてみると、同様にして DF1=DF2=(長半径) であることもわかります。

　次に、三角形BOF1について考えてみると、これは直角三角形なので三平方の定理より

{(BF1)}^{2} = {(OB)}^{2} + {(OF1)}^{2}

→

OF1 = \sqrt{{(BF1)}^{2} - {(OB)}^{2}}

ここで、 BF1=(長半径)、OB=(短半径) なので、

OF1 = \sqrt{{(長半径)}^{2} - {(短半径)}^{2}}

となる。

　　

　説明図3では、(長半径)=a 、 (短半径)=b の楕円を考え、焦点F1のx座標をmとしています。
各点の座標はそれぞれ、

只今、作成中です。